質量欠損・E＝mc2…核融合のエネルギー[Q&A-10]

2024年9月15日

URLをコピーしました！

この記事では、質量欠損をE=mc²を使って計算しながら、核融合や核分裂といった核反応のエネルギーの大きさがどれくらいか、解説します。

記事Q&A-7では、核融合や核分裂といった「核反応」と、「化学反応」の違いについて説明しました。また、その記事の最後に、「核反応では化学反応の数万倍以上のエネルギーが出る」とも記載しました。（どういうことを前提とした計算の仕方をするかで、何万、何十万、何百万倍になるかは異なります。）

これはつまり、私たちが日常的に扱っていて「熱い！」と感じる炎なんかよりも、原子力発電所の中ではとんでもないエネルギーが発生していることになります。

なぜ、核反応でそのような膨大なエネルギーが出るのか。この記事で解説していきたいと思います。この記事の終わりまでに、「質量欠損」という言葉を覚えてもらえたらと思います。

核融合・核分裂といった「核反応」と「化学反応」の違い（Q&A-7話の続き）

エネルギーの話の前に、核反応と化学反応の違いについて、Q&A-7話に引き続き説明したいことがあるので、ここで少し解説します。

（まだ、こちらの記事を読まれてない場合は、読んでみて下さい）

Q&A-７話では、次の図を使って、「化学反応」は原子のチーム替えと説明しました。

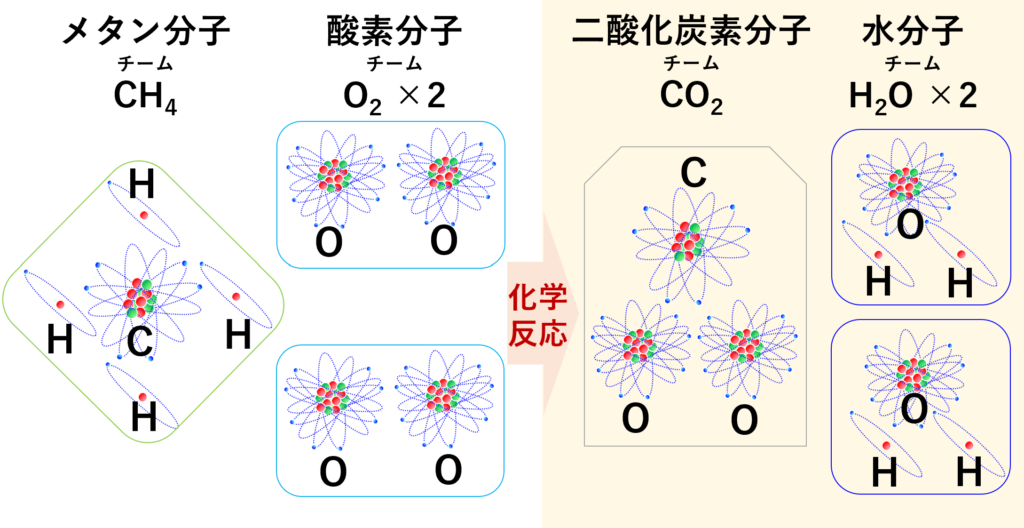
一方、核融合や核分裂といった、「核反応」の前後では、全く別人の原子ができると説明しました。

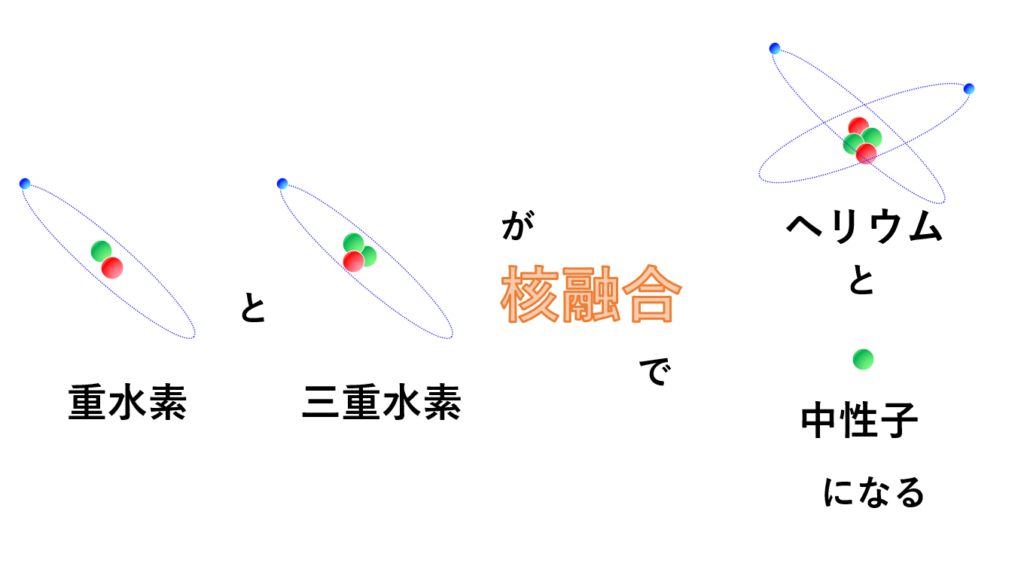
重水素と三重水素の核融合 — 核融合や核分裂といった核反応では、まるで別人が生まれるかのように、別の原子ができる

質量欠損…核反応の前後で、重さが変わる？

ここで、化学反応の前後と、核反応の前後の、「重さの変化」に着目してみたいと思います。

化学反応の場合、原子がチーム替えするだけなので、反応前と反応後で重さは変わりません。

一方、核反応の前後はどうなるのかというと、実は核反応の前より核反応した後の方が、なんとほーんの少しだけ軽くなるのです。これを「質量欠損」と言います。

核融合や核分裂といった、核反応の「後」にできた原子の重さの合計は、反応前の原子の重さの合計よりも軽くなる。この現象を、質量欠損（しつりょうけっそん）という。

これはつまり、例えば核融合の例を見てみると、重水素と三重水素が核融合してヘリウムと中性子になる場合、重さは（重水素＋三重水素）＞（ヘリウム＋中性子）ということになります。

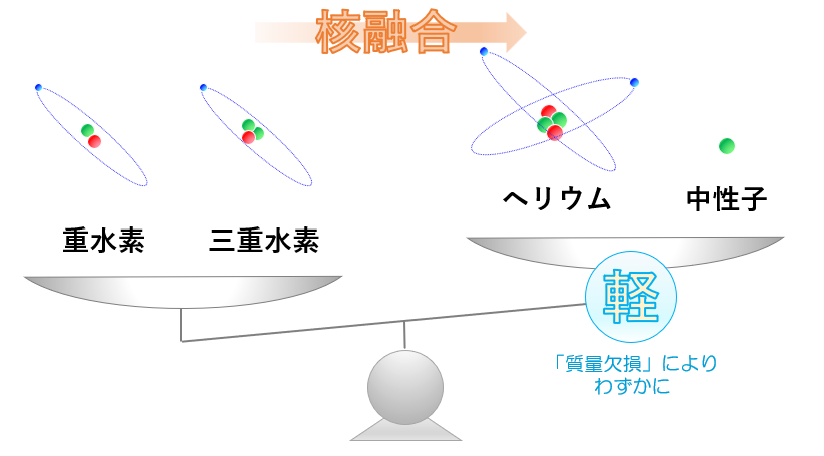
果たして、本当にそうなのでしょうか？実際に、これ以降で解説していきます。

なお、物理学では、物質本来の重さのことを「質量」（しつりょう）と言います。聞き慣れないかもしれませんが、覚えておいて下さい。

核融合の質量欠損を例に

核融合反応の前後で、原子の重さは（重水素＋三重水素）＞（ヘリウム＋中性子）なのかどうか、調べてみましょう。重水素と三重水素の原子が1個ずつ核融合した場合を考えます。すると、以下のようになります。

＜核融合反応「前」の原子の重さ：重水素+三重水素の重さ＞

重水素の原子1個の重さ＝ 3.3445 × 10^-27 kg
三重水素の原子1個の重さ = 5.0083 × 10^-27 kg
重水素+三重水素の重さの合計 = 8.3528 × 10^-27 kg

＜核融合反応「後」の原子の重さ：ヘリウム+中性子の重さ＞

ヘリウムの原子1個の重さ＝ 6.6466 × 10^-27 kg
中性子1個の重さ＝1.6749 × 10^-27 kg
ヘリウム＋中性子の重さの合計＝8.3215 × 10^-27 kg

× 10^-27 kg があると分かりづらいですが、核融合前の「8.3528」と、核融合後の「8.3215」を比べると、0.0313× 10^-27 kg だけ、後の方が軽いことが分かります。

確かに、わずかだけ重さが（重水素＋三重水素）＞（ヘリウム＋中性子）となっていて、質量欠損が起きているのです。

核反応の前後で、質量欠損があっても、陽子・中性子・電子の合計数は変わらない

ここで注意してもらいたいのは、核融合や核分裂では、陽子・中性子・電子の合計数は、反応の前後で変わらないということです。

例えばこの、重水素・三重水素 → ヘリウム・中性子の核融合反応の例で,
それぞれの種類の原子が持つ陽子・中性子・電子の数を書くと、次の表のようになります。

	陽子の数（個）	中性子の数（個）	電子の数
重水素	1	1	1
三重水素	1	2	1
ヘリウム	2	2	2
中性子	0	1	0

これを見ると、核融合反応の前と後で、陽子・中性子・電子の数が変わっていないことがわかります。

では、なぜ、核融合反応後に重さが軽くなっているのでしょうか？

◆2024年～核融合の先生閲覧数　＞＞　現在 27,768 回閲覧されています！◆

質量欠損で軽くなった分の重さは、莫大エネルギーになる！　E＝mc2

実は核反応の後、このように原子の重さが「質量欠損」によって軽くなるとき、減った質量の分だけ莫大なエネルギーが放出されるのです。

ところで、皆さんは “E＝mc²” という式をご存知でしょうか？

これは、かの天才物理学者アインシュタインが導き出した式のうちの一つです。最近の週間少年ジャンプのマンガ「Dr. STONE」で、主人公の服にも書かれていましたね。

E=mc2と書かれた服を着るDr. STONEの主人公 — 引用元：「Dr.STONE」公式（@DrSTONE_off）さん / Twitter

この式: E=mc²は、核反応で（質量欠損が起こるときに）生じるエネルギー：E を計算するときに使われます。

そして、この計算をしてみると、「核反応」のエネルギーは、「化学反応」のエネルギーなんて足元にも及ばないくらい莫大だということが分かったのです。

E=mc²を実際に使って、核反応の質量欠損で生じるエネルギーを求めてみる

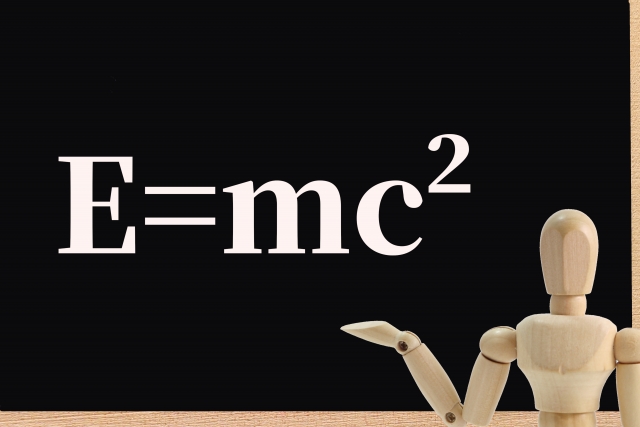
E＝mc²　とは、つまり、　
（核反応で生じるエネルギー: E）= （質量欠損で軽くなった分の重さ：m）×（光の速さ：c）×（光の速さ：c）

言葉でもう少し分かりやすく言うと、「Eは、質量欠損で軽くなった分の重さに、光の速さを2回掛け算すると計算できます」ということです。

実際にこの式を使って、「核反応」のエネルギーを簡単に求めてみましょう。再び、核融合を題材にして、

質量欠損
質量欠損から生じるエネルギー

を計算します。

核融合の「質量欠損」を簡単に計算してみた

重水素と三重水素が核融合して、ヘリウムが6.6466グラムできた場合を例題とします。

計算をしやすくするため、少し中途半端な数字ですが、先ほどの計算パートで使った、各原子の重さに数値を合わせます。大体、1円玉1枚が1グラムですので、1円玉6枚半くらいの重さが、この6.6466グラムと思ってください。

これだけのヘリウムが作られるためには、重水素が3.3445グラム、三重水素が5.0083グラム必要になります。
また、この核融合反応のときは、ヘリウムと同時に中性子が、1.6749グラム作られます。

さて、核融合の前後で、重さを比べてみましょう。

核融合反応前（重水素＋三重水素）＝　3.3445　+　5.0083 = 8.3528 グラム
　　　反応後（ヘリウム＋中性子）＝　6.6466　+　1.6749 = 8.3215 グラム

このようになり、核融合の後で0.0313グラム減っているのです。

核融合のエネルギーを計算してみた

それでは、0.0313グラムの質量が減ったとき、どれだけのエネルギー：Eが出るか、E=mc²を使って計算してみましょう。

mは質量欠損の0.0313グラムですが、この式を使うときはキログラムに直さないといけないルールなので、m=0.0000313（キログラム）となります。

cは光の速さで、秒速3億メートルです。c=300,000,000 m/sとなります。

E=　0.0000313　×　300,000,000　×　300,000,000
≒　3,000,000,000,000　ジュール（おおよそ）となります。約3兆ジュールということです。

この3兆ジュールが、重水素と三重水素を合計で8.3528グラム（約8グラム）を核融合させ、質量欠損で0.0313グラムの重さが減ったときに生じる、核融合のエネルギーなのです。

質量欠損から生じるエネルギーはすごいの？

ただ、3兆ジュールって言われても、すごいかどうがわかりませんね。
そこで、3兆ジュールのエネルギーで、どれだけの量のお湯が沸かせるかを考えてみます。

水は、1グラムを1℃上げるのに、4.2ジュール必要です。ということは、1グラムの水を0℃から100℃に上げるには、その100倍の420ジュールが必要です。

では、何グラムの水を0℃から100℃に上げられるかは、3兆ジュールを420ジュールで割れば答えがでます。そして、

3兆÷420 ≒7,000,000,000　グラムの水を沸騰させることができる、という計算結果になりました。これをもう少し分かりやすく言うと、7千トンです。

7千トンは、ピンときますか？例えば、体重100 kg（100 kgは0.1トン）の体が大きい人が、7万人いたとします。この大人数と同じだけの重さの冷水を、沸騰したお湯に変えることができるんです。1円玉たった8枚分くらいの重水素と三重水素の混合燃料を、核融合させるだけで。

たったこれだけの燃料で、これだけのエネルギーを出すのは、「化学反応」ではできません。だからこそ、核反応のエネルギーは莫大だと言えるのです。

姉妹サイト「副業支援の先生」

エンジニア・研究職・文系専門職向けの副業ノウハウを発信中。

✅リンク 副業支援の先生 (http://side-job-help.com)

そもそも、なぜ質量欠損が起こる？

解説を飛ばしていましたが、そもそもなぜ「質量欠損」が起きるのか。陽子・中性子・電子の数は変わっていないのに。

実は、筆者も上手くお伝えすることができません。（スミマセン…。）これを上手く説明するためには、原子よりもさらに小さな粒子である「素粒子」を勉強したり、「相対性理論」を学んだりすることが必要です。

かたちあるものすべては、最初からただのエネルギーの塊？

1つ言えるのは、重さとエネルギーは表裏のような関係があるということです。私たちは、普段生きていて、何気なく「かたちあるもの」に触れたりしていますが、そもそもなぜ、私たち生命も含めて「かたちあるもの」があるか不思議に思いませんが？だって、「かたちあるもの」があるということは、切っても切ってもその下に何かないといけません。ちょうど、こけしやマトリョーシカのように。

一昔前は、「かたちあるもの」を構成する最小単位は「原子」と言われていました。ですが最近では、「原子」を構成しているのは、それよりさらに小さい「素粒子」だと言われ、研究が進められています。しかし、じゃあ素粒子を構成するのは何か。さらにそれを構成するのは何か。この問いは無限にできます。むしろどこかで、「ふたを開けたら何もなかった」ことがわかったりしたら、どうなるのか。怖いですね。

とすると、私たち生命も含め、宇宙にある「かたちあるものすべては、最初からただのエネルギーの塊」なのかもしれません（？）。 E=mc²という式は、「エネルギー: E」と「かたちあるもの: m」はイコールだ！ということを示してくれています。ですが、この解釈のためには、工学分野を超えた勉強が必要です。